ENERGÍA CINÉTICA.
La energía cinética de un objeto depende tanto de su masa como de su rapidez, es decir, es igual al producto de la mitad de la masa por el cuadrado de su rapidez:
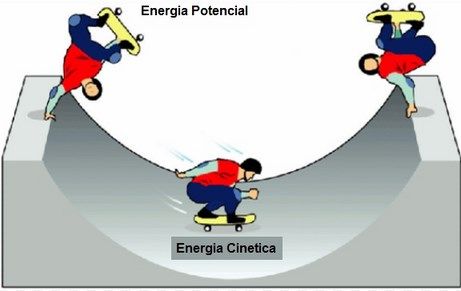
Ec=m/2 × v^2
PRESIÓN
La presión que un gas ejerce sobre las paredes de un recipiente se debe a la fuerza que resulta del cambio de cantidad de movimiento de las moléculas de un gas con choques elásticos contra la pared. La fuerza ejercida por un molécula individual es igual a la tasa de cambio de la cantidad de movimiento con el tiempo, es decir:
F=∆p/∆t
La suma de los componentes normales instantáneos de las fuerzas de choque origina la presión promedio sobre la pared.
Por las leyes del movimiento de Newton, es posible calcular la fuerza ejercida sobre las paredes del recipiente, a partir del cambio de cantidad de movimiento de las moléculas de un gas cuando chocan contra las paredes. En términos de presión (fuerza/área):
pV=1/3 Nmv^2
V: es el volumen del recipiente o gas
N: número de moléculas de gas en el recipiente cerrado
m: masa de un molécula de gas
v: rapidez promedio de las moléculas
Para calcular la fuerza a todas las moléculas en el contenedor, se tiene que sumar las aportaciones de cada una. La fuerza neta sobre la pared es
F=m/l (v^2x1 + v^2x2 + ....+v^2xN)
Donde
vx1 significa vx
para la molécula 1 (a cada molécula se le asigna arbitrariamente un número) y la suma se extiende sobre el número total de moléculas N en el contenedor. El valor promedio del componente z de la velocidad es
V^2=v^2x1 + v^2x2 + ....+v^2xN/N
por tanto la fuerza se puede escribir como
F= (m/l) Nv^2x
Se sabe que el cuadrado de cualquier vector es igual a la suma de los cuadrados de sus componentes (teorema de Pitágoras).
v^2= v^2 x + v^2 y + v^2 z
En consecuencia, para cualquier velocidad v. Al tomar los promedios se obtiene
v^2= v^2x + v^2y + v^2z
Las moléculas en el gas se suponen aleatorias. Al combinar esta relación con la anterior, se obtiene:
v^2= 3v^2x
Se sustituye en la ecuación para la fuerza neta F
F= (m/l) N (v^2/3)
donde V= lA es el volumen del contenedor. Esta es la presión ejercida por un gas sobre su contenedor expresada en términos de propiedades moleculares.
Si se supone que colisión es inelástica solo cambia el componente x de la cantidad en movimiento de la molécula y cambia de mvx ( se mueve en la dirección x negativa) a +mvx. Por tanto el cambio en la cantidad de movimiento de la molécula que es la cantidad de movimiento final menos la cantidad de movimiento inicial para una colisión.
Esta molécula realizara muchas colisiones con la pared, cada una separada por un tiempo t, que es el tiempo que toma la molécula viajar a través del contenedor y regresar de nuevo, una distancia (componente x) igual a 2l.
El tiempo t entre colisiones es muy pequeño, de modo que el número de colisiones por segundo es muy grande.
TEMPERATURA
Si despejamos pV de la ecuación 1e igualamos la ecuación resultante da la ecuación número 2 veremos cómo es que la temperatura se interpreta como una medida de la energía cinética traslacional
La temperatura de un gas ( y de las paredes del recipiente o de un bulbo de termómetro en equilibrio térmico con el gas) es directamente proporcional a su energía cinética aleatoria promedio ( por molécula)
En Termodinámica como una variable que se mide por los cambios observados en las propiedades macroscópicas de la materia cuando cambia la temperatura. La ecuación de estado de un gas ideal relaciona las propiedades macroscópicas, presión P, el volumen V y temperatura T.
PV=RT
Siendo el número de moles. El número n de moléculas por unidad de volumen se obtiene dividiendo el número total de moléculas N entre elvolumen del recipiente V.
donde N0 el número de Avogadro. Suele redondearse como 6,022 x 10 elevado a 23 y recibe el nombre de número de Avogadro (en ocasiones presentado como constante de Avogadro) en honor al científico de nacionalidad italiana Amedeo Avogadro (1776-1856), quien también formuló la ley que afirma que, en condiciones iguales de temperatura y presión, volúmenes idénticos de gases diferentes poseen igual cantidad de partículas
Para mayor información puedes consultar los siguientes links: http://www.educaplus.org/gases/tcm_y_p.html y http://www.educaplus.org/gases/tcm_y_t.html
Si despejamos pV de la ecuación 1e igualamos la ecuación resultante da la ecuación número 2 veremos cómo es que la temperatura se interpreta como una medida de la energía cinética traslacional
La temperatura de un gas ( y de las paredes del recipiente o de un bulbo de termómetro en equilibrio térmico con el gas) es directamente proporcional a su energía cinética aleatoria promedio ( por molécula)
En Termodinámica como una variable que se mide por los cambios observados en las propiedades macroscópicas de la materia cuando cambia la temperatura. La ecuación de estado de un gas ideal relaciona las propiedades macroscópicas, presión P, el volumen V y temperatura T.
PV=RT
Siendo el número de moles. El número n de moléculas por unidad de volumen se obtiene dividiendo el número total de moléculas N entre elvolumen del recipiente V.
donde N0 el número de Avogadro. Suele redondearse como 6,022 x 10 elevado a 23 y recibe el nombre de número de Avogadro (en ocasiones presentado como constante de Avogadro) en honor al científico de nacionalidad italiana Amedeo Avogadro (1776-1856), quien también formuló la ley que afirma que, en condiciones iguales de temperatura y presión, volúmenes idénticos de gases diferentes poseen igual cantidad de partículas
Para mayor información puedes consultar los siguientes links: http://www.educaplus.org/gases/tcm_y_p.html y http://www.educaplus.org/gases/tcm_y_t.html

No hay comentarios.:
Publicar un comentario