Descripción Empírica del Movimiento Browniano

Una de las primeras descripciones macroscópicas del movimiento browniano fue hecha en 1908 por el físico francés Paul Langevin. Él hizo las siguientes consideraciones: si una partícula grande (comparada con las dimensiones atómicas) se introduce en un fluido, entonces, de acuerdo con la hidrodinámica, va a experimentar una fuerza opuesta que depende de su velocidad. Como ejemplo de este hecho podemos mencionar el caso de un auto o de un aeroplano que se mueven: el aire genera una fuerza que se opone al movimiento; o cuando nadamos en una alberca: el agua se opone a nuestro movimiento. Esta fuerza de oposición se debe a la viscosidad del fluido. Mientras mayor sea la velocidad con que se mueve el cuerpo dentro del fluido, mayor será la fuerza de oposición, o de fricción viscosa, que se genere.

Por otro lado, de lo descrito anteriormente se sabe que al introducir una partícula grande dentro de un fluido, aquélla experimenta fuerzas debidas a las colisiones que sufre con las moléculas del fluido. En vista de la gran cantidad de colisiones que ocurren en cada instante, esta segunda fuerza varía de una forma muy azarosa y violenta. Ello significa que si, por ejemplo, hacemos observaciones de la partícula browniana con una escala de tiempo del orden de los segundos la fuerza debida a las colisiones variará mucho, pues en un segundo habrán ocurrido muchísimas colisiones. Por otro lado, en esta misma escala de tiempo, la primera fuerza de la que hemos hablado, la de fricción, varía muy poco.

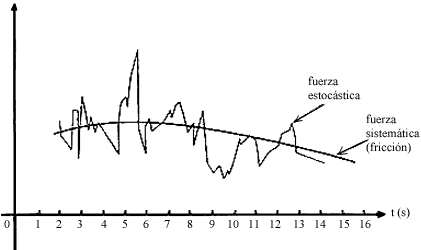
La siguiente imagen muestra que las fuerzas estocástica y viscosa que experimenta la partícula browniana varían en diferentes escalas de tiempo.

De esta manera, se reconocen dos escalas de tiempo muy distintas: la escala en la que varía la fuerza de fricción (que es, para casos típicos, del orden de segundos) y la escala en la que varía la fuerza debida a las colisiones (que es del orden de milésimas de microsegundo). Esto significa que si observamos los fenómenos con escalas de tiempo de segundos, la fuerza de fricción apenas cambia, mientras que la otra fuerza ya habrá cambiado muchísimas veces.

Ahora bien, si se conoce la velocidad de la partícula, la fuerza de fricción también se puede determinar: es proporcional a ella. Es decir, si la velocidad aumenta al doble, la fuerza se duplica; si la velocidad se triplica la fuerza aumenta al triple, etcétera. El coeficiente de proporcionalidad entre la fuerza y la velocidad depende de la viscosidad del fluido así como de la forma geométrica de la partícula. Estas dependencias son conocidas aunque no las daremos aquí. Además, el sentido que tiene la fuerza es opuesto al de la velocidad ya que aquélla se opone al movimiento (Figura 11). En otras palabras, es posible determinar completamente esta fuerza en cada instante. En la teoría del movimiento browniano se suele llamar fuerza sistemática a esta fuerza de fricción.

Otra cosa ocurre con la fuerza debida a las colisiones. Dado que en un segundo el número de colisiones que experimenta la partícula browniana con las del fluido es enorme, resulta prácticamente imposible determinar el valor exacto de esta fuerza en cualquier instante. Por la misma causa, este valor varía en pequeños intervalos, de manera impredecible. Estamos entonces ante una situación en que una de las fuerzas que experimenta la partícula browniana varía de manera azarosa; es decir, se tiene una fuerza fluctuante. En matemáticas este tipo de cantidad recibe el nombre de estocástica.

La siguiente imagen, hace referencia a que La fuerza viscosa tiene sentido opuesto a la velocidad de la partícula.

Bibliografía:

Eliezer Braun. (1986). Un movimiento en Zigzag. México: Fondo de Cultura Económica.

Importancia del Movimiento Browniano en la comprobación de la Teoría Cinética de la Materia

En el año de 1828 el botánico inglés  Robert Brown observó que en una solución de agua el polen de cierta hierba (Clarkia pulchella) realizaba un  movimiento continuo, muy accidentado, en zigzag. Al examinar estas partículas y después de observaciones repetidas se convenció de que estos movimiento no surgían de corrientes en el fluido, ni de su gradual evaporación, sino que pertenecían a la misma partícula. 
Gracias a esto se logró concluir para ese momento que el movimiento que lleva a cabo una partícula muy pequeña que está inmersa en un fluido, se llama movimiento Browniano, este movimiento se caracteriza por ser continuo y muy irregular.
La siguiente imagen, muestra de manera clara como es la trayectoria que sigue una partícula en el movimiento Browniano:

Con ayuda de lo mencionado anteriormente y de los puntos ya expuestos en el blog, les expondremos como el Movimiento Browniano tiene de gran importancia en la comprobación de la Teoría Cinética de la Materia.

Pero primero, queremos mostrar un vídeo donde quedará claro de mejor manera qué es el movimiento Browniano, dicho video fue tomado del portal de vídeos de Youtube (https://www.youtube.com/watch?v=IL4atcvxpWE)

Hacia mediados del siglo XIX se enfrentaba la siguiente situación: por un lado, se habían planteado las leyes de la termodinámica que, se referían a aspectos macroscópicos del comportamiento de las sustancias; y por el otro lado, ya se tenía un cuerpo de teoría adecuado, aunque incompleto que implicaba que la materia estaba compuesta de partículas microscópicas, llamadas átomos.  

Entonces ante la necesidad de conciliar estos dos conocimientos, se planteó la siguiente cuestión: si la materia, en efecto, está compuesta de partículas microscópicas, ¿qué consecuencias macroscópicas tiene el comportamiento microscópico de una sustancia?

Gracias a esto entre 1850 y 1875 Agust Krönig (1822-1879) Rudolf Clausius, James C. Maxwell (1831-1879) y Ludwing Boltzmann (1844-1906) desarrollaron las bases de la moderna teoría cinética de la materia. Supusieron que las sustancias estaban compuestas de átomos y a partir de su comportamiento microscópico obtuvieron como consecuencia algunas propiedades macroscópicas.

Igualmente hacia mediados del siglo XIX se habían formado muchas hipótesis del Movimiento Browniano, en particular se pudo probar de manera contundente que este movimiento no se debía a que hubiera diferencias de temperatura entre dos regiones del espacio. El movimiento browniano se presenta también cuando la temperatura es la misma en todos los puntos del fluido. En 1863 Wiener formuló varios argumentos para mostrar que el movimiento browniano no podía atribuirse a causas externas, sino que tenía que deberse a movimientos internos del fluido. Asimismo, Cantoni lo atribuyó a movimientos térmicos en el líquido, y consideró que este fenómeno nos daba una demostración experimental, bella y directa, de los principios fundamentales de la teoría mecánica del calor.

Como se ha ido explicando para estos tiempos ya se hablaba de que las partículas que componían las sustancias se movían, combinando así la materia y los estados de está con el movimiento browniano. Algunas personas consideraron la posibilidad de que el movimiento browniano fuera causado por las colisiones de los átomos del fluido con la partícula inmersa en él. El botánico alemán Karl Nägeli publicó un trabajo en 1879 en el que trató de probar que este mecanismo no podía ser el causante del movimiento browniano. Para ello, usó las estimulaciones de las masas y velocidades de los átomos que se habían obtenido de la teoría cinética para calculas los cambios en la velocidad que experimenta la partícula browniana después de una colisión con un átomo del fluido. El químico inglés William Ramsay llego simultáneamente a la misma conclusión y argumento que la partícula inmersa en el fluido tiene una masa mucho mayor que la de un átomo del fluido entonces al chocar estas dos partículas, la partícula masiva casi no es afectada por el choque. 

La siguiente imagen muestra que las velocidades de los átomos de un fluido tienen una variedad en direcciones.

En el año de 1905 el físico Albert Einstein público un célebre trabajo el que propuso la explicación del movimiento browniano. El artículo se titulaba "Sobre el movimiento de pequeñas partículas suspendidas en líquidos en reposo requerido por la teoría cinético-molecular del calor" 

En este trabajo describió el movimiento de las moléculas suspendidas en un líquido, y que quizás este fenómeno era idéntico a un fenómeno químico del que había oído hablar, el movimiento browniano. Con ayuda de ese punto de partida, continuó demostrando que podía usar las teorías del calor en vigor para describir cómo el calor, incluso a temperatura ambiente, provocaría que las moléculas del líquido estuviesen en continuo movimiento. Este movimiento haría a su vez que cualquier partícula suspendida en el líquido resultase empujada. Einstein obtuvo además de conclusiones cualitativas predicciones cuantitativas que podrían compararse con resultados experimentales. Entre estas predicciones destacan dos muy importantes: predijo la distancia que debe recorrer una partícula suspendida en un fluido y además mostró que la segunda ley de la termodinámica se cumple sólo en promedio.
Albert Einstein, imagen lateral, fue un personaje que ofreció su explicación acerca del movimiento Browiano, y la siguiente imagen nos muestra dicha explicación.

Bibliografía:

Eliezer Braun. (1986). Un movimiento en Zigzag. México: Fondo de Cultura Económica.

https://www.youtube.com/watch?v=IL4atcvxpWE

Deducción matemática de la presión y temperatura bajo la Teoría cinética molecular

ENERGÍA CINÉTICA.

La energía cinética de un objeto depende tanto de su masa como de su rapidez, es decir, es igual al producto de la mitad de la masa por el cuadrado de su rapidez:  

Ec=m/2 × v^2

Si aún cuerpo se le duplica su rapidez, entonces su energía se cuadruplica.

PRESIÓN

La presión que un gas ejerce sobre las paredes de un recipiente se debe a la fuerza que resulta del cambio de cantidad de movimiento de las moléculas de un gas con choques elásticos  contra la pared. La fuerza ejercida por un molécula individual es igual  a la tasa de cambio de la cantidad de movimiento con el tiempo, es decir: 

    F=∆p/∆t

La suma de los componentes normales instantáneos de las fuerzas de choque origina la  presión promedio sobre la pared.

Por las leyes del movimiento de Newton, es posible calcular la fuerza ejercida sobre las paredes del recipiente, a partir del cambio de cantidad de movimiento de las moléculas de un gas cuando chocan contra las paredes. En términos de presión (fuerza/área):

pV=1/3 Nmv^2

                                               

Dónde:
V: es el volumen del recipiente o gas
N: número de moléculas de gas en el recipiente cerrado
m: masa de un molécula de gas
v: rapidez promedio de las moléculas

Para calcular la fuerza a todas las moléculas en el contenedor, se tiene que sumar las aportaciones de cada una. La fuerza neta sobre la pared es

                   F=m/l (v^2x1 + v^2x2 + ....+v^2xN)

                         

Donde

vx1 significa vx

para la molécula 1 (a cada molécula se le asigna arbitrariamente un número) y la suma se extiende sobre el número total de moléculas N en el contenedor. El valor promedio del componente z de la velocidad es

V^2=v^2x1 + v^2x2 + ....+v^2xN/N

por tanto la fuerza se puede escribir como

                                                          F= (m/l)  Nv^2x                                                                                      

Se sabe que el cuadrado de  cualquier vector es igual a la suma de los cuadrados de sus componentes (teorema de Pitágoras). 

v^2= v^2 x + v^2 y + v^2 z

En consecuencia, para cualquier velocidad v. Al tomar los promedios se obtiene 

v^2= v^2x + v^2y + v^2z

Las moléculas en el gas se suponen aleatorias. Al combinar esta relación con la anterior, se obtiene:

v^2= 3v^2x

Se sustituye en la ecuación para la fuerza neta F 

F= (m/l) N (v^2/3)

donde V= lA es el volumen del contenedor. Esta es la presión ejercida por un gas sobre su contenedor expresada en términos de propiedades moleculares.

Si se supone que colisión es inelástica solo cambia el componente x de la cantidad en movimiento de la molécula y cambia de mvx ( se mueve en la dirección x negativa) a +mvx. Por tanto el cambio en la cantidad de movimiento de la molécula que es la cantidad de movimiento final menos la cantidad de movimiento inicial  para una colisión.

 Esta molécula realizara muchas colisiones  con la pared, cada una separada por un tiempo t, que es el tiempo que toma la molécula viajar a través del contenedor y regresar de nuevo, una distancia (componente x) igual a 2l.

El tiempo t entre colisiones es muy pequeño, de modo que el número de colisiones por segundo es muy grande.

TEMPERATURA

Si despejamos pV de la ecuación 1e igualamos la ecuación resultante da la ecuación número 2 veremos cómo es que la temperatura se interpreta como una medida de la energía cinética traslacional
La temperatura de un gas ( y de las paredes del recipiente o de un bulbo de termómetro en equilibrio térmico con el gas) es directamente proporcional  a su energía cinética aleatoria promedio ( por molécula)                                                 
En Termodinámica como una variable que se mide por los cambios observados en las propiedades macroscópicas de la materia cuando cambia la temperatura. La ecuación de estado de un gas ideal relaciona las propiedades macroscópicas, presión P, el volumen V y temperatura T.
                                                                            PV=RT
Siendo  el número de moles. El número n de moléculas por unidad de volumen se obtiene dividiendo el número total de moléculas N entre elvolumen del recipiente V.


donde N0 el número de Avogadro. Suele redondearse como 6,022 x 10 elevado a 23 y recibe el nombre de número de Avogadro (en ocasiones presentado como constante de Avogadro) en honor al científico de nacionalidad italiana Amedeo Avogadro (1776-1856), quien también formuló la ley que afirma que, en condiciones iguales de temperatura y presión, volúmenes idénticos de gases diferentes poseen igual cantidad de partículas

Para mayor información puedes consultar los siguientes links: http://www.educaplus.org/gases/tcm_y_p.html y http://www.educaplus.org/gases/tcm_y_t.html